Exploring Floyd's Cycle-Finding Algorithm: Detecting Repeating Patterns in Python

Introduction:

In the world of computer science, algorithms play a crucial role in solving complex problems efficiently. One such algorithm, Floyd's Cycle-Finding Algorithm, is used to detect cycles in linked lists or sequences. It provides an elegant and efficient solution to this problem and has various applications in areas like graph theory, optimization, and more. In this article, we will explore the concept behind Floyd's Cycle-Finding Algorithm and how it works step by step.

Understanding the Problem:

Before diving into the algorithm itself, let's define the problem it aims to solve. Given a linked list, we want to determine if there is a cycle within it. A cycle occurs when a node in the list points to a previous node, creating a loop. Detecting cycles is crucial in various scenarios, such as identifying infinite loops in programs or finding repetitive patterns in data structures.

Floyd's Cycle-Finding Algorithm:

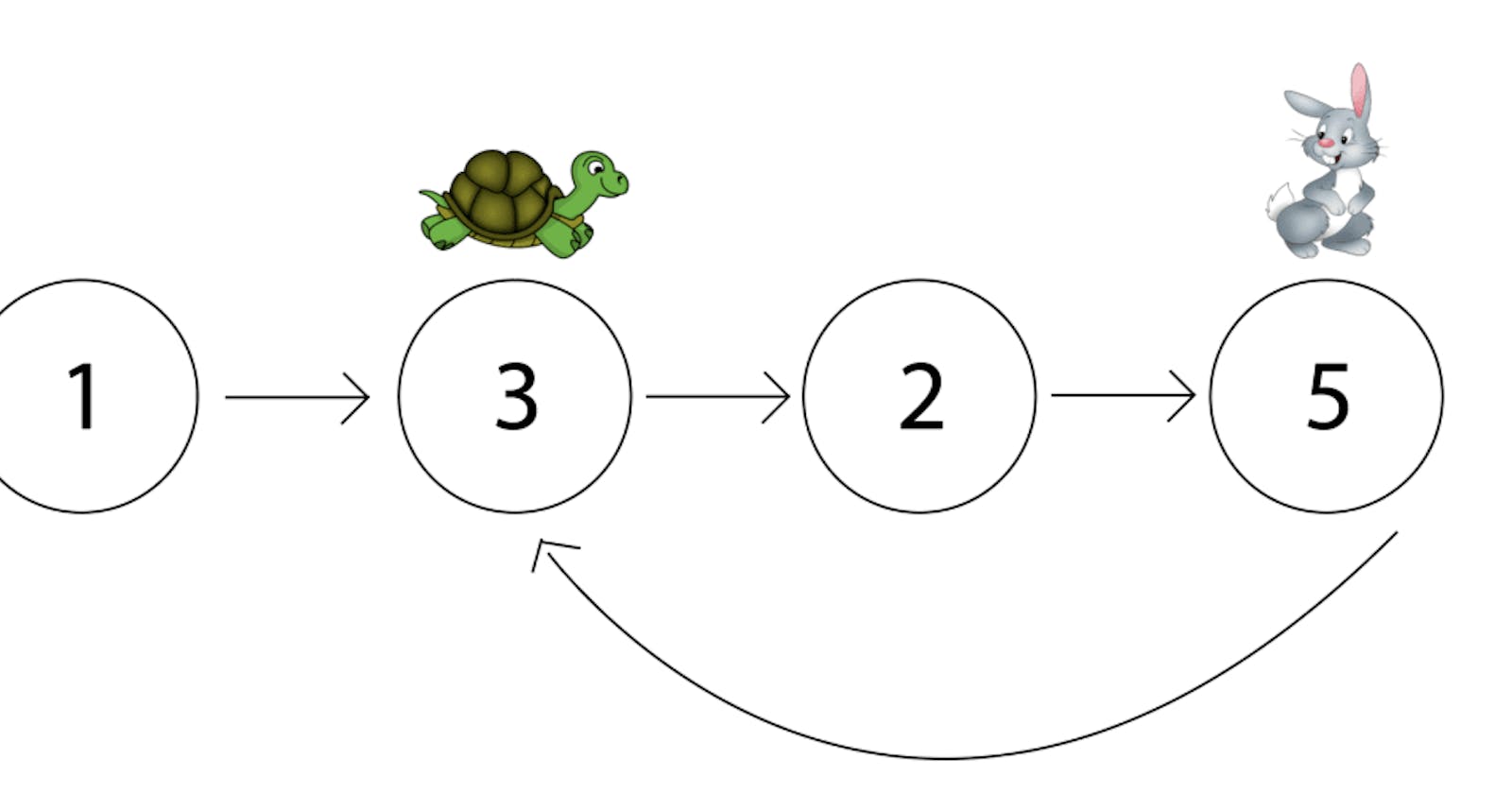
Floyd's Cycle-Finding Algorithm, also known as the Tortoise and Hare Algorithm, is a two-pointer technique used to detect cycles in linked lists. The algorithm takes advantage of the speed difference between two pointers to identify if a cycle exists. Here's how it works:

1. Initialize two pointers, often called the slow pointer and the fast pointer, and point them to the head of the linked list.

2. Move the slow pointer one step at a time and the fast pointer two steps at a time.

3. If there is no cycle in the linked list, the fast pointer will eventually reach the end (i.e., become NULL) because it moves twice as fast as the slow pointer.

4. If there is a cycle, the fast pointer will eventually catch up to the slow pointer as they traverse the loop.

5. If the two pointers meet at any point during the traversal, it confirms the presence of a cycle in the linked list.

Visualization:

To better understand the algorithm, let's visualize it with a simple example. Consider the following linked list with a cycle:

   +---+    +---+    +---+
   | A | -> | B | -> | C |
   +---+    +---+    +---+
             ^         |
             |         v
             +-------- D

In this example, the node labeled "D" points back to node "B," creating a cycle. Now, let's apply Floyd's Cycle-Finding Algorithm to detect this cycle:

1. Initialize the slow pointer (S) and the fast pointer (F) to the head of the linked list, pointing to node "A."

2. Move S one step forward to node "B" and F two steps forward to node "C."

3. Move S to node "C" and F to node "D."

4. Move S to node "D" and F back to node "B," completing one cycle.

5. Repeat the process until the two pointers meet at node "B," confirming the presence of a cycle.

Applications and Time Complexity:

Floyd's Cycle-Finding Algorithm has various applications in computer science. Apart from detecting cycles in linked lists, it is used in graph algorithms, cycle detection in sequences, memory management systems, and more.

In terms of time complexity, the algorithm runs in linear time O(n), where n is the length of the linked list. The pointers traverse the list at different speeds, but the worst-case scenario occurs when there is a cycle, and the fast pointer catches up to the slow pointer after going around the loop once.

Solving a Problem with Floyd's Cycle-Finding Algorithm in Python:

Let's apply Floyd's Cycle-Finding Algorithm to solve a real-world problem. Consider a scenario where you have a list of integers, and you need to determine if there is a repeating pattern within the list. This problem can be solved by detecting cycles using Floyd's Cycle-Finding Algorithm. Here's how you can implement it in Python:

def find_repeating_pattern(nums):
    slow = nums[0]  # Initialize the slow pointer
    fast = nums[0]  # Initialize the fast pointer

    while True:
        slow = nums[slow]  # Move the slow pointer one step
        fast = nums[nums[fast]]  # Move the fast pointer two steps

        if slow == fast:
            break  # Cycle detected, exit the loop

    # Move slow back to the starting point and increment both pointers at the same pace
    slow = nums[0]
    while slow != fast:
        slow = nums[slow]
        fast = nums[fast]

    return slow  # Return the repeating pattern

# Example usage
numbers = [1, 2, 3, 4, 2, 5, 6, 3, 4]
repeating_pattern = find_repeating_pattern(numbers)
if repeating_pattern is not None:
    print("The repeating pattern is:", repeating_pattern)
else:
    print("No repeating pattern found.")

In this example, we define a function find_repeating_pattern that takes a list of integers nums. We initialize two pointers, slow and fast, to the first element of the list. Then, we move the pointers through the list using the same logic as in Floyd's Cycle-Finding Algorithm. If a cycle is detected (i.e., the pointers meet at the same element), we break out of the loop.

After detecting the cycle, we reset the slow pointer back to the starting point and increment both pointers at the same pace until they meet again. The element at which they meet represents the repeating pattern within the list.

Finally, we print the repeating pattern if one is found, or a message indicating that no repeating pattern was found.

By applying Floyd's Cycle-Finding Algorithm, we can efficiently solve problems that involve detecting repeating patterns or cycles within sequences or lists.

Related video:

Conclusion:

Floyd's Cycle-Finding Algorithm provides an efficient solution to detect cycles in linked lists. Its simplicity and effectiveness make it a popular choice in various applications. By understanding the concept behind this algorithm, you can tackle cycle detection problems more effectively and optimize your algorithms accordingly.

Remember, the next time you encounter a linked list or a sequence and need to determine if it contains a cycle, you can rely on Floyd's Cycle-Finding Algorithm to provide an elegant solution.

Happy coding!

Twitter